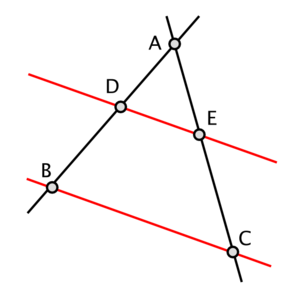
Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odpowiednie odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta.
Dla powyższych rysunków zachodzi: 

lub po przekształceniu:  oraz
oraz  a także
a także  .
.
 oraz
oraz  a także
a także  .
.
Często spotykaną nieścisłością jest takie formułowanie twierdzenia Talesa: 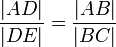 , ta równość jest prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.
, ta równość jest prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.
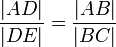 , ta równość jest prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.
, ta równość jest prawdziwa, ale wynika z podobieństwa trójkątów ADE i ABC a nie z samego twierdzenia Talesa.
Dowód oparty jest na dwóch lematach:
- Jeśli dwa trójkąty mają równe wysokości, to stosunek ich pól jest równy stosunkowi długości ich podstaw.
- Jeśli dwa trójkąty mają wspólną podstawę i równe wysokości, to ich pola są równe.
- Dowód
Niech ![[ABC]](http://upload.wikimedia.org/math/f/b/f/fbf29c161428aa651110db2c6230f2b9.png) oznacza pole powierzchni trójkąta
oznacza pole powierzchni trójkąta 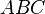 .
.
![[ABC]](http://upload.wikimedia.org/math/f/b/f/fbf29c161428aa651110db2c6230f2b9.png) oznacza pole powierzchni trójkąta
oznacza pole powierzchni trójkąta 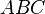 .
.
Trójkąty  i
i  mają wspólną wysokość
mają wspólną wysokość 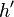 , więc na mocy lematu 1.:
, więc na mocy lematu 1.:
 i
i  mają wspólną wysokość
mają wspólną wysokość 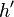 , więc na mocy lematu 1.:
, więc na mocy lematu 1.:![\frac{|CE|}{|EA|} = \frac{[CED]}{[EAD]}](http://upload.wikimedia.org/math/a/1/2/a124358d7b4c9edba8e5d9a876ec31db.png) .
.
Dodatkowo trójkąty  i
i  mają wspólną podstawę
mają wspólną podstawę  i równe wysokości
i równe wysokości  , dlatego na mocy lematu 2:
, dlatego na mocy lematu 2:
 i
i  mają wspólną podstawę
mają wspólną podstawę  i równe wysokości
i równe wysokości  , dlatego na mocy lematu 2:
, dlatego na mocy lematu 2:![[CED] = [BDE]\;](http://upload.wikimedia.org/math/9/c/1/9c13cc094c966c62d10e3f79eca6d2e4.png) , stąd
, stąd ![\frac{[CED]}{[EAD]} = \frac{[BDE]}{[EAD]}](http://upload.wikimedia.org/math/8/d/5/8d5f6ac10ea00d80fc2c031a10184fd7.png) .
.
Trójkąty  i
i  mają wspólną wysokość, więc zgodnie z lematem 1:
mają wspólną wysokość, więc zgodnie z lematem 1:
 i
i  mają wspólną wysokość, więc zgodnie z lematem 1:
mają wspólną wysokość, więc zgodnie z lematem 1:![\frac{[BDE]}{[EAD]} = \frac{|BD|}{|DA|}](http://upload.wikimedia.org/math/0/2/f/02f5348d0bcc3a6b432706e9abea1860.png) .
.
Przyrównując do siebie te równości otrzymuje się
![\frac{|CE|}{|EA|} = \frac{[CED]}{[EAD]} = \frac{[BDE]}{[EAD]} = \frac{|BD|}{|DA|}](http://upload.wikimedia.org/math/1/d/7/1d7077ee1a44669dc8221e9104561f84.png) ,
,
czego należało dowieść.

Brak komentarzy:
Prześlij komentarz